info asymptote

7.27 `three`

This module fully extends the notion of guides and paths in Asymptote to three dimensions. It introduces the new types guide3, path3, and surface. Guides in three dimensions are specified with the same syntax as in two dimensions except that triples (x,y,z) are used in place of pairs (x,y) for the nodes and direction specifiers. This generalization of John Hobby's spline algorithm is shape-invariant under three-dimensional rotation, scaling, and shifting, and reduces in the planar case to the two-dimensional algorithm used in Asymptote, MetaPost, and MetaFont [cf. J. C. Bowman, Proceedings in Applied Mathematics and Mechanics, 7:1, 2010021-2010022 (2007)].

For example, a unit circle in the XY plane may be filled and drawn like this:

import three;

size(100);

path3 g=(1,0,0)..(0,1,0)..(-1,0,0)..(0,-1,0)..cycle;
draw(g);
draw(O--Z,red+dashed,Arrow3);
draw(((-1,-1,0)--(1,-1,0)--(1,1,0)--(-1,1,0)--cycle));
dot(g,red);

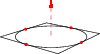and then distorted into a saddle:

import three;

size(100,0);
path3 g=(1,0,0)..(0,1,1)..(-1,0,0)..(0,-1,1)..cycle;
draw(g);
draw(((-1,-1,0)--(1,-1,0)--(1,1,0)--(-1,1,0)--cycle));
dot(g,red);

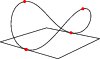
Bezier surfaces, the natural two-dimensional generalization of Bezier curves, are shaded using the OpenGL lighting scheme, which uses the Phong-Blinn specular model. Sample Bezier surfaces are contained in the example files BezierSurface.asy, teapot.asy, and parametricsurface.asy.

Bezier surfaces are also used to draw arbitrary thick three-dimensional lines and line caps (which the OpenGL standard does not require implementations to provide). This can make files slow to render, especially with the Adobe Reader renderer. The setting thick=false can be used to disable this feature and force all lines to be drawn with linewidth(0) (one pixel wide, regardless of the resolution). By default mesh and contour lines in three-dimensions are always drawn thin, unless an explicit linewidth is given in the pen parameter or the setting thin is set to false. The pens thin() and thick() defined in plain_pens.asy can also be used to override these defaults for specific draw commands.

There is no fill command for arbitrary three-dimensional cyclic paths (this would be an ill-posed operation). A three-dimensional planar path constructed from a two-dimensional cyclic path p can be filled by using Orest Shardt's bezulate routine to decompose p into an array of cyclic paths of length 4 or less; these can then be used to construct and draw a (filled) planar surface:

draw(surface(bezulate(polygon(5))),red);
draw(surface(bezulate(unitcircle)),red);

Alternatively, the routine surface planar(path3 p) can be used to convert any planar three-dimensional path to a surface. We also provide constructors for converting two-dimensional paths to three-dimensional ones, and vice-versa:

path3 path3(path p, triple plane(pair)=XYplane);
path path(path3 p, pair P(triple)=xypart);

There are four choices for viewing 3D Asymptote output:

Use the default Asymptote adaptive OpenGL-based renderer (with the the command-line option -V and the default settings outformat="" and render=-1). An initial screen position can be specified with the pair setting position, where negative values are interpreted as relative to the corresponding maximum screen dimension. The mouse bindings are:
- Left: rotate
- shift Left: zoom
- ctrl Left: shift
- Middle: menu
- Wheel: zoom
- Right: zoom
- Right double click: menu
- shift Right: rotate about the X axis
- ctrl Right: rotate about the Y axis
- alt Right: rotate about the Z axis
The keyboard shortcuts are:
- h: home
- f: toggle fitscreen
- x: spin about the X axis
- y: spin about the Y axis
- z: spin about the Z axis
- s: stop spinning
- m: rendering mode (solid/mesh/patch)
- e: export
- +: expand
- =: expand
- -: shrink
- _: shrink
- q: exit
- Ctrl-q: exit
Render the scene to a specified rasterized format outformat at the resolution of n pixels per bp, as specified by the setting render=n. A negative value of n is interpreted as |4n| for EPS and PDF formats and |2n| for other formats. The default value of render is -1.
Embed the 3D PRC format in a PDF file (using the setting outformat="pdf" and the default setting prc=true) and view the resulting PDF file with version 8.0 or later of Adobe Reader. This requires version 2008/10/08 or later of the movie15 package from
http://www.ctan.org/tex-archive/macros/latex/contrib/movie15

A stationary preview image with a resolution of n pixels per bp can be embedded with the setting render=n; this allows the file to be viewed with other PDF viewers. Alternatively, the file externalprc.tex illustrates how the resulting PRC and rendered image files can be extracted and processed in a separate LaTeX file. However, see LaTeX usage for an easier way to embed three-dimensional Asymptote pictures within LaTeX. The open-source PRC specification is available from http://www.adobe.com/cfusion/entitlement/index.cfm?e=acrobat_prc_spec
Project the scene to a two-dimensional vector (EPS or PDF) format with render=0. Only limited hidden surface removal facilities are currently available with this approach (see 3DPostScript).

Automatic picture sizing in three dimensions is accomplished with double deferred drawing. The maximal desired dimensions of the scene in each of the three dimensions can optionally be specified with the routine

void size3(picture pic=currentpicture, real x, real y=x, real z=y,
          bool keepAspect=pic.keepAspect);

The resulting simplex linear programming problem is then solved to produce a 3D version of a frame (actually implemented as a 3D picture). The result is then fit with another application of deferred drawing to the viewport dimensions corresponding to the usual two-dimensional picture size parameters.

For convenience, the three module defines O=(0,0,0), X=(1,0,0), Y=(0,1,0), and Z=(0,0,1), along with a unitcircle in the XY plane:

path3 unitcircle3=X..Y..-X..-Y..cycle;

A general (approximate) circle can be drawn perpendicular to the direction normal with the routine

path3 circle(triple c, real r, triple normal=Z);

A circular arc centered at c with radius r from c+r*dir(theta1,phi1) to c+r*dir(theta2,phi2), drawing counterclockwise relative to the normal vector cross(dir(theta1,phi1),dir(theta2,phi2)) if theta2 > theta1 or if theta2 == theta1 and phi2 >= phi1, can be constructed with

path3 arc(triple c, real r, real theta1, real phi1, real theta2, real phi2,
          triple normal=O);

The normal must be explicitly specified if c and the endpoints are colinear. If r < 0, the complementary arc of radius |r| is constructed. For convenience, an arc centered at c from triple v1 to v2 (assuming |v2-c|=|v1-c|) in the direction CCW (counter-clockwise) or CW (clockwise) may also be constructed with

path3 arc(triple c, triple v1, triple v2, triple normal=O,
          bool direction=CCW);

When high accuracy is needed, the routines Circle and Arc defined in graph3 may be used instead. See GaussianSurface for an example of a three-dimensional circular arc.

The representation O--O+u--O+u+v--O+v--cycle of the plane passing through point O with normal cross(u,v) is returned by

path3 plane(triple u, triple v, triple O=O);

A three-dimensional box with opposite vertices at triples v1 and v2 may be drawn with the function

path3[] box(triple v1, triple v2);

For example, a unit box is predefined as

path3[] unitbox=box(O,(1,1,1));

Asymptote also provides optimized definitions for the three-dimensional paths unitsquare3 and unitcircle3, along with the surfaces unitdisk, unitplane, unitcube, unitcylinder, unitcone, unitsolidcone, unitfrustum(real t1, real t2), unitsphere, and unithemisphere.

These projections to two dimensions are predefined:

oblique
oblique(real angle): The point (x,y,z) is projected to (x-0.5z,y-0.5z). If an optional real argument is given, the negative z axis is drawn at this angle in degrees. The projection obliqueZ is a synonym for oblique.
obliqueX
obliqueX(real angle): The point (x,y,z) is projected to (y-0.5x,z-0.5x). If an optional real argument is given, the negative x axis is drawn at this angle in degrees.
obliqueY
obliqueY(real angle): The point (x,y,z) is projected to (x+0.5y,z+0.5y). If an optional real argument is given, the positive y axis is drawn at this angle in degrees.
orthographic(triple camera, triple up=Z): This projects from three to two dimensions using the view as seen at a point infinitely far away in the direction unit(camera), orienting the camera so that, if possible, the vector up points upwards. Parallel lines are projected to parallel lines.
orthographic(real x, real y, real z, triple up=Z): This is equivalent to orthographic((x,y,z),up).
perspective(triple camera, triple up=Z, triple target=O): This projects from three to two dimensions, taking account of perspective, as seen from the location camera looking at target, orienting the camera so that, if possible, the vector up points upwards. If render=0, projection of three-dimensional cubic Bezier splines is implemented by approximating a two-dimensional nonuniform rational B-spline (nurbs) with a two-dimensional Bezier curve containing additional nodes and control points.
perspective(real x, real y, real z, triple up=Z, triple target=O): This is equivalent to perspective((x,y,z),up,target).

The default projection, currentprojection, is initially set to perspective(5,4,2).

A triple or path3 can be projected to a pair or path, with project(triple, projection P=currentprojection) or project(path3, projection P=currentprojection).

It is occasionally useful to be able to invert a projection, sending a pair z onto the plane perpendicular to normal and passing through point:

triple invert(pair z, triple normal, triple point,
              projection P=currentprojection);

A pair direction dir can be inverted to a triple direction relative to a point v with the routine

triple invert(pair dir, triple v, projection P=currentprojection).

Three-dimensional objects may be transformed with one of the following built-in transform3 types:

shift(triple v): translates by the triple v;
xscale3(real x): scales by x in the x direction;
yscale3(real y): scales by y in the y direction;
zscale3(real z): scales by z in the z direction;
scale3(real s): scales by s in the x, y, and z directions;
scale(real x, real y, real z): scales by x in the x direction, by y in the y direction, and by z in the z direction;
rotate(real angle, triple v): rotates by angle in degrees about an axis v through the origin;
rotate(real angle, triple u, triple v): rotates by angle in degrees about the axis u--v;
reflect(triple u, triple v, triple w): reflects about the plane through u, v, and w.

Three-dimensional TeX Labels, which are by default drawn as Bezier surfaces directly on the projection plane, can be transformed from the XY plane by any of the above transforms or mapped to a specified two-dimensional plane with the transform3 types XY, YZ, ZX, YX, ZY, ZX. There are also modified versions of these transforms that take an optional argument projection P=currentprojection that rotate and/or flip the label so that it is more readable from the initial viewpoint.

A transform3 that projects in the direction dir onto the plane with normal n through point O is returned by

transform3 planeproject(triple n, triple O=O, triple dir=n);

As illustrated in the example planeproject.asy, a transform3 that projects in the direction dir onto the plane defined by a planar path p is returned by

transform3 planeproject(path3 p, triple dir=normal(p));

Three-dimensional versions of the path functions length, size, point, dir, accel, radius, precontrol, postcontrol, arclength, arctime, reverse, subpath, intersect, intersections, intersectionpoint, intersectionpoints, min, max, cyclic, and straight are also defined.

Here is an example showing all five guide3 connectors:

import graph3;

size(200);

currentprojection=orthographic(500,-500,500);

triple[] z=new triple[10];

z[0]=(0,100,0); z[1]=(50,0,0); z[2]=(180,0,0);

for(int n=3; n <= 9; ++n)
  z[n]=z[n-3]+(200,0,0);

path3 p=z[0]..z[1]---z[2]::{Y}z[3]
&z[3]..z[4]--z[5]::{Y}z[6]
&z[6]::z[7]---z[8]..{Y}z[9];

draw(p,grey+linewidth(4mm)+opacity(0.5));

xaxis3(Label(XY()*"$x$",align=-3Y),red,Above);
yaxis3(Label(XY()*"$y$",align=-3X),red,Above);

dot(z);

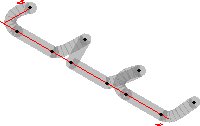
Three-dimensional versions of arrows can be drawn with one of the specifiers None, Blank, BeginArrow3, MidArrow3, EndArrow3 (or equivalently Arrow3), and Arrows3. The predefined three-dimensional arrowhead styles are DefaultHead3, HookHead3, TeXHead3.

Further three-dimensional examples are provided in the files near_earth.asy, conicurv.asy, and (in the animations subdirectory) cube.asy.

Limited support for projected vector graphics (effectively three-dimensional nonrendered PostScript) is also available by specifying settings.render=0. This currently only works for piecewise planar surfaces, such as those produced by the parametric surface routines in the graph3 module. Surfaces produced by the solids package will also be properly rendered if the parameter nslices is sufficiently large.

In the module bsp, hidden surface removal of planar pictures is implemented using a binary space partition and picture clipping. A planar path is first converted to a structure face derived from picture. A face may be given to a two-dimensional drawing routine in place of any picture argument. An array of such faces may then be drawn, removing hidden surfaces:

void add(picture pic=currentpicture, face[] faces,
         projection P=currentprojection);

Labels may be projected to two dimensions, using projection P, onto the plane passing through point O with normal cross(u,v) by multiplying it on the left by the transform

transform transform(triple u, triple v, triple O=O,
                    projection P=currentprojection);

Here is an example that shows how a binary space partition may be used to draw a PostScript vector image of three orthogonal intersecting planes:

size(6cm,0);
import bsp;

real u=2.5;
real v=1;

currentprojection=oblique;

path3 y=plane((2u,0,0),(0,2v,0),(-u,-v,0));
path3 l=rotate(90,Z)*rotate(90,Y)*y;
path3 g=rotate(90,X)*rotate(90,Y)*y;

face[] faces;
filldraw(faces.push(y),project(y),yellow);
filldraw(faces.push(l),project(l),lightgrey);
filldraw(faces.push(g),project(g),green);

add(faces);

[ < ]

[ > ]

[ << ]

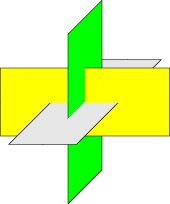
[ Up ]

[ >> ]

[Top]

[Contents]

[Index]

[ ? ]

7.27 three

7.27 `three`