6.2 Paths and guides

path

a cubic spline resolved into a fixed path. The implicit initializer for paths is nullpath.

For example, the routine circle(pair c, real r), which returns a Bezier curve approximating a circle of radius r centered on c, is based on unitcircle (see unitcircle):

path circle(pair c, real r)
{
  return shift(c)*scale(r)*unitcircle;
}

If high accuracy is needed, a true circle may be produced with the routine Circle defined in the module graph.asy:

import graph;
path Circle(pair c, real r, int n=nCircle);

A circular arc consistent with circle centered on c with radius r from angle1 to angle2 degrees, drawing counterclockwise if angle2 >= angle1, can be constructed with

path arc(pair c, real r, real angle1, real angle2);

One may also specify the direction explicitly:

path arc(pair c, real r, real angle1, real angle2, bool direction);

Here the direction can be specified as CCW (counter-clockwise) or CW (clockwise). For convenience, an arc centered at c from pair z1 to z2 (assuming |z2-c|=|z1-c|) in the may also be constructed with

path arc(pair c, explicit pair z1, explicit pair z2,
         bool direction=CCW)

If high accuracy is needed, true arcs may be produced with routines in the module graph.asy that produce Bezier curves with n control points:

import graph;
path Arc(pair c, real r, real angle1, real angle2, bool direction,
         int n=nCircle);
path Arc(pair c, real r, real angle1, real angle2, int n=nCircle);
path Arc(pair c, explicit pair z1, explicit pair z2,
         bool direction=CCW, int n=nCircle);

An ellipse can be drawn with the routine

path ellipse(pair c, real a, real b)
{
  return shift(c)*scale(a,b)*unitcircle;
}

A brace can be constructed between pairs a and b with

path brace(pair a, pair b, real amplitude=bracedefaultratio*length(b-a));

This example illustrates the use of all five guide connectors discussed in Tutorial and Bezier curves:

size(300,0);
pair[] z=new pair[10];

z[0]=(0,100); z[1]=(50,0); z[2]=(180,0);

for(int n=3; n <= 9; ++n)
  z[n]=z[n-3]+(200,0);

path p=z[0]..z[1]---z[2]::{up}z[3]
&z[3]..z[4]--z[5]::{up}z[6]
&z[6]::z[7]---z[8]..{up}z[9];

draw(p,grey+linewidth(4mm));

dot(z);

Here are some useful functions for paths:

int length(path p);

This is the number of (linear or cubic) segments in path p. If p is cyclic, this is the same as the number of nodes in p.

int size(path p);

This is the number of nodes in the path p. If p is cyclic, this is the same as length(p).

bool cyclic(path p);

returns true iff path p is cyclic.

bool straight(path p, int i);

returns true iff the segment of path p between node i and node i+1 is straight.

bool piecewisestraight(path p)

returns true iff the path p is piecewise straight.

pair point(path p, int t);

If p is cyclic, return the coordinates of node t mod length(p). Otherwise, return the coordinates of node t, unless t < 0 (in which case point(0) is returned) or t > length(p) (in which case point(length(p)) is returned).

pair point(path p, real t);

This returns the coordinates of the point between node floor(t) and floor(t)+1 corresponding to the cubic spline parameter t-floor(t) (see section Bezier curves). If t lies outside the range [0,length(p)], it is first reduced modulo length(p) in the case where p is cyclic or else converted to the corresponding endpoint of p.

pair dir(path p, int t, int sign=0, bool normalize=true);

If sign < 0, return the direction (as a pair) of the incoming tangent to path p at node t; if sign > 0, return the direction of the outgoing tangent. If sign=0, the mean of these two directions is returned.

pair dir(path p, real t, bool normalize=true);

returns the direction of the tangent to path p at the point between node floor(t) and floor(t)+1 corresponding to the cubic spline parameter t-floor(t) (see section Bezier curves).

pair dir(path p)

returns dir(p,length(p)).

pair dir(path p, path q)

returns unit(dir(p)+dir(q)).

pair accel(path p, int t, int sign=0);

If sign < 0, return the acceleration of the incoming path p at node t; if sign > 0, return the acceleration of the outgoing path. If sign=0, the mean of these two accelerations is returned.

pair accel(path p, real t);

returns the acceleration of the path p at the point t.

real radius(path p, real t);

returns the radius of curvature of the path p at the point t.

pair precontrol(path p, int t);

returns the precontrol point of p at node t.

pair precontrol(path p, real t);

returns the effective precontrol point of p at parameter t.

pair postcontrol(path p, int t);

returns the postcontrol point of p at node t.

pair postcontrol(path p, real t);

returns the effective postcontrol point of p at parameter t.

real arclength(path p);

returns the length (in user coordinates) of the piecewise linear or cubic curve that path p represents.

real arctime(path p, real L);

returns the path "time", a real number between 0 and the length of the path in the sense of point(path p, real t), at which the cumulative arclength (measured from the beginning of the path) equals L.

real arcpoint(path p, real L);

returns point(p,arctime(p,L)).

real dirtime(path p, pair z);

returns the first "time", a real number between 0 and the length of the path in the sense of point(path, real), at which the tangent to the path has the direction of pair z, or -1 if this never happens.

real reltime(path p, real l);

returns the time on path p at the relative fraction l of its arclength.

pair relpoint(path p, real l);

returns the point on path p at the relative fraction l of its arclength.

pair midpoint(path p);

returns the point on path p at half of its arclength.

path reverse(path p);

returns a path running backwards along p.

path subpath(path p, int a, int b);

returns the subpath of p running from node a to node b. If a < b, the direction of the subpath is reversed.

path subpath(path p, real a, real b);

returns the subpath of p running from path time a to path time b, in the sense of point(path, real). If a < b, the direction of the subpath is reversed.

real[] intersect(path p, path q, real fuzz=-1);

If p and q have at least one intersection point, return a real array of length 2 containing the times representing the respective path times along p and q, in the sense of point(path, real), for one such intersection point (as chosen by the algorithm described on page 137 of The MetaFontbook). The computations are performed to the absolute error specified by fuzz, or if fuzz < 0, to machine precision. If the paths do not intersect, return a real array of length 0.

real[][] intersections(path p, path q, real fuzz=-1);

Return all (unless there are infinitely many) intersection times of paths p and q as a sorted array of real arrays of length 2 (see sort). The computations are performed to the absolute error specified by fuzz, or if fuzz < 0, to machine precision.

real[] intersections(path p, explicit pair a, explicit pair b, real fuzz=-1);

Return all (unless there are infinitely many) intersection times of path p with the (infinite) line through points a and b as a sorted array. The intersections returned are guaranteed to be correct to within the absolute error specified by fuzz, or if fuzz < 0, to machine precision.

real[] times(path p, real x)

returns all intersection times of path p with the vertical line through (x,0).

real[] times(path p, explicit pair z)

returns all intersection times of path p with the horizontal line through (0,z.y).

real[] mintimes(path p)

returns an array of length 2 containing times at which path p reaches its minimal horizontal and vertical extents, respectively.

real[] maxtimes(path p)

returns an array of length 2 containing times at which path p reaches its maximal horizontal and vertical extents, respectively.

pair intersectionpoint(path p, path q, real fuzz=-1);

returns the intersection point point(p,intersect(p,q,fuzz)[0]).

pair[] intersectionpoints(path p, path q, real fuzz=-1);

returns an array containing all intersection points of the paths p and q.

pair extension(pair P, pair Q, pair p, pair q);

returns the intersection point of the extensions of the line segments P--Q and p--q, or if the lines are parallel, (infinity,infinity).

slice cut(path p, path knife, int n);

returns the portions of path p before and after the nth intersection of p with path knife as a structure slice (if no intersection exist is found, the entire path is considered to be ‘before’ the intersection):

struct slice {
  path before,after;
}

The argument n is treated as modulo the number of intersections.

slice firstcut(path p, path knife);

equivalent to cut(p,knife,0); Note that firstcut.after plays the role of the MetaPost cutbefore command.

slice lastcut(path p, path knife);

equivalent to cut(p,knife,-1); Note that lastcut.before plays the role of the MetaPost cutafter command.

path buildcycle(... path[] p);

This returns the path surrounding a region bounded by a list of two or more consecutively intersecting paths, following the behaviour of the MetaPost buildcycle command.

pair min(path p);

returns the pair (left,bottom) for the path bounding box of path p.

pair max(path p);

returns the pair (right,top) for the path bounding box of path p.

int windingnumber(path p, pair z);

returns the winding number of the cyclic path p relative to the point z. The winding number is positive if the path encircles z in the counterclockwise direction. If z lies on p the constant undefined (defined to be the largest odd integer) is returned.

bool interior(int windingnumber, pen fillrule)

returns true if windingnumber corresponds to an interior point according to fillrule.

bool inside(path p, pair z, pen fillrule=currentpen);

returns true iff the point z lies inside or on the edge of the region bounded by the cyclic path p according to the fill rule fillrule (see fillrule).

int inside(path p, path q, pen fillrule=currentpen);

returns 1 if the cyclic path p strictly contains q according to the fill rule fillrule (see fillrule), -1 if the cyclic path q strictly contains p, and 0 otherwise.

pair inside(path p, pen fillrule=currentpen);

returns an arbitrary point strictly inside a cyclic path p according to the fill rule fillrule (see fillrule).

real orient(pair a, pair b, pair c);

returns a positive (negative) value if a--b--c--cycle is oriented counterclockwise (clockwise) or zero if all three points are colinear. Equivalently, a positive (negative) value is returned if c lies to the left (right) of the line through a and b or zero if c lies on this line. The value returned is the determinant

|a.x a.y 1|
|b.x b.y 1|
|c.x c.y 1|

real incircle(pair a, pair b, pair c, pair d);

returns a positive (negative) value if d lies inside (outside) the circle passing through the counterclockwise-oriented points a,b,c or zero if d lies on the this circle. The value returned is the determinant

|a.x a.y a.x^2+a.y^2 1|
|b.x b.y b.x^2+b.y^2 1|
|c.x c.y c.x^2+c.y^2 1|
|d.x d.y d.x^2+d.y^2 1|

path[] strokepath(path g, pen p=currentpen);

returns the path array that PostScript would fill in drawing path g with pen p.

guide

an unresolved cubic spline (list of cubic-spline nodes and control points). The implicit initializer for a guide is nullpath; this is useful for building up a guide within a loop.

A guide is similar to a path except that the computation of the cubic spline is deferred until drawing time (when it is resolved into a path); this allows two guides with free endpoint conditions to be joined together smoothly. The solid curve in the following example is built up incrementally as a guide, but only resolved at drawing time; the dashed curve is incrementally resolved at each iteration, before the entire set of nodes (shown in red) is known:

size(200);

real mexican(real x) {return (1-8x^2)*exp(-(4x^2));}

int n=30;
real a=1.5;
real width=2a/n;

guide hat;
path solved;

for(int i=0; i < n; ++i) {
  real t=-a+i*width;
  pair z=(t,mexican(t));
  hat=hat..z;
  solved=solved..z;
}

draw(hat);
dot(hat,red);
draw(solved,dashed);

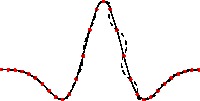
We point out an efficiency distinction in the use of guides and paths:

guide g;
for(int i=0; i < 10; ++i)
  g=g--(i,i);
path p=g;

runs in linear time, whereas

path p;
for(int i=0; i < 10; ++i)
  p=p--(i,i);

runs in quadratic time, as the entire path up to that point is copied at each step of the iteration.

The following routines can be used to examine the individual elements of a guide without actually resolving the guide to a fixed path (except for internal cycles, which are resolved):

int size(guide g);

Analogous to size(path p).

int length(guide g);

Analogous to length(path p).

bool cyclic(path p);

Analogous to cyclic(path p).

pair point(guide g, int t);

Analogous to point(path p, int t).

guide reverse(guide g);

Analogous to reverse(path p). If g is cyclic and also contains a secondary cycle, it is first solved to a path, then reversed. If g is not cyclic but contains an internal cycle, only the internal cycle is solved before reversal. If there are no internal cycles, the guide is reversed but not solved to a path.

pair[] dirSpecifier(guide g, int i);

This returns a pair array of length 2 containing the outgoing (in element 0) and incoming (in element 1) direction specifiers (or (0,0) if none specified) for the segment of guide g between nodes i and i+1.

pair[] controlSpecifier(guide g, int i);

If the segment of guide g between nodes i and i+1 has explicit outgoing and incoming control points, they are returned as elements 0 and 1, respectively, of a two-element array. Otherwise, an empty array is returned.

tensionSpecifier tensionSpecifier(guide g, int i);

This returns the tension specifier for the segment of guide g between nodes i and i+1. The individual components of the tensionSpecifier type can be accessed as the virtual members in, out, and atLeast.

real[] curlSpecifier(guide g);

This returns an array containing the initial curl specifier (in element 0) and final curl specifier (in element 1) for guide g.

As a technical detail we note that a direction specifier given to nullpath modifies the node on the other side: the guides

a..{up}nullpath..b;
c..nullpath{up}..d;
e..{up}nullpath{down}..f;

are respectively equivalent to

a..nullpath..{up}b;
c{up}..nullpath..d;
e{down}..nullpath..{up}f;

This document was generated on May 24, 2014 using texi2html 5.0.