| [ << ] | [ < ] | [ Up ] | [ > ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
5 Bezier curves
Each interior node of a cubic spline may be given a
direction prefix or suffix {dir}: the direction of the pair
dir specifies the direction of the incoming or outgoing tangent,
respectively, to the curve at that node. Exterior nodes may be
given direction specifiers only on their interior side.
A cubic spline between the node z_0, with postcontrol point c_0, and the node z_1, with precontrol point c_1, is computed as the Bezier curve
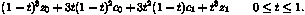
As illustrated in the diagram below, the third-order midpoint (m_5) constructed from two endpoints z_0 and z_1 and two control points c_0 and c_1, is the point corresponding to t=1/2 on the Bezier curve formed by the quadruple (z_0, c_0, c_1, z_1). This allows one to recursively construct the desired curve, by using the newly extracted third-order midpoint as an endpoint and the respective second- and first-order midpoints as control points:
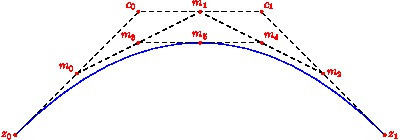
Here m_0, m_1 and m_2 are the first-order midpoints, m_3 and m_4 are the second-order midpoints, and m_5 is the third-order midpoint. The curve is then constructed by recursively applying the algorithm to (z_0, m_0, m_3, m_5) and (m_5, m_4, m_2, z_1).
In fact, an analogous property holds for points located at any fraction t in [0,1] of each segment, not just for midpoints (t=1/2).
The Bezier curve constructed in this manner has the following properties:
- It is entirely contained in the convex hull of the given four points.
- It starts heading from the first endpoint to the first control point and finishes heading from the second control point to the second endpoint.
The user can specify explicit control points between two nodes like this:
draw((0,0)..controls (0,100) and (100,100)..(100,0));
However, it is usually more convenient to just use the
.. operator, which tells Asymptote to choose its own
control points using the algorithms described in Donald Knuth’s
monograph, The MetaFontbook, Chapter 14.
The user can still customize the guide (or path) by specifying
direction, tension, and curl values.
The higher the tension, the straighter the curve is, and the more it approximates a straight line. One can change the spline tension from its default value of 1 to any real value greater than or equal to 0.75 (cf. John D. Hobby, Discrete and Computational Geometry 1, 1986):
draw((100,0)..tension 2 ..(100,100)..(0,100)); draw((100,0)..tension 3 and 2 ..(100,100)..(0,100)); draw((100,0)..tension atleast 2 ..(100,100)..(0,100));
In these examples there is a space between 2 and ...
This is needed as 2. is interpreted as a numerical constant.
The curl parameter specifies the curvature at the endpoints of a path (0 means straight; the default value of 1 means approximately circular):
draw((100,0){curl 0}..(100,100)..{curl 0}(0,100));
The MetaPost ... path connector, which requests, when possible, an
inflection-free curve confined to a triangle defined by the
endpoints and directions, is implemented in Asymptote as the
convenient abbreviation :: for ..tension atleast 1 ..
(the ellipsis ... is used in Asymptote to indicate a
variable number of arguments; see section Rest arguments). For example,
compare
draw((0,0){up}..(100,25){right}..(200,0){down});

with
draw((0,0){up}::(100,25){right}::(200,0){down});

The --- connector is an abbreviation for ..tension atleast
infinity.. and the & connector concatenates two paths, after
first stripping off the last node of the first path (which normally
should coincide with the first node of the second path).
| [ << ] | [ < ] | [ Up ] | [ > ] | [ >> ] | [Top] | [Contents] | [Index] | [ ? ] |
This document was generated on May 24, 2014 using texi2html 5.0.
