29.2 Voronoi Diagrams

A Voronoi diagram or Voronoi tessellation of a set of points s in an N-dimensional space, is the tessellation of the N-dimensional space such that all points in v(p), a partitions of the tessellation where p is a member of s, are closer to p than any other point in s. The Voronoi diagram is related to the Delaunay triangulation of a set of points, in that the vertexes of the Voronoi tessellation are the centers of the circum-circles of the simplicies of the Delaunay tessellation.

Function File: voronoi (x, y)

Function File: voronoi (x, y, "plotstyle")

Function File: voronoi (x, y, "plotstyle", options)

Function File: [vx, vy] = voronoi (…)

plots voronoi diagram of points (x, y). The voronoi facets with points at infinity are not drawn. [vx, vy] = voronoi(…) returns the vertices instead of plotting the diagram. plot (vx, vy) shows the voronoi diagram.

A fourth optional argument, which must be a string, contains extra options passed to the underlying qhull command. See the documentation for the Qhull library for details.

x = rand (10, 1); y = rand (size (x)); h = convhull (x, y); [vx, vy] = voronoi (x, y); plot (vx, vy, "-b", x, y, "o", x(h), y(h), "-g") legend ("", "points", "hull");

See also: voronoin, delaunay, convhull.

Function File: [C, F] = voronoin (pts)

Function File: [C, F] = voronoin (pts, options)

computes n- dimensional voronoi facets. The input matrix pts of size [n, dim] contains n points of dimension dim. C contains the points of the voronoi facets. The list F contains for each facet the indices of the voronoi points.

A second optional argument, which must be a string, contains extra options passed to the underlying qhull command. See the documentation for the Qhull library for details.

See also: voronoin, delaunay, convhull.

An example of the use of voronoi is

rand("state",9);
x = rand(10,1);
y = rand(10,1);
tri = delaunay (x, y);
[vx, vy] = voronoi (x, y, tri);
triplot (tri, x, y, "b");
hold on;
plot (vx, vy, "r");

Additional information about the size of the facets of a Voronoi diagram, and which points of a set of points is in a polygon can be had with the polyarea and inpolygon functions respectively.

Function File: polyarea (x, y)

Function File: polyarea (x, y, dim)

Determines area of a polygon by triangle method. The variables x and y define the vertex pairs, and must therefore have the same shape. They can be either vectors or arrays. If they are arrays then the columns of x and y are treated separately and an area returned for each.

If the optional dim argument is given, then polyarea works along this dimension of the arrays x and y.

An example of the use of polyarea might be

rand ("state", 2);
x = rand (10, 1);
y = rand (10, 1);
[c, f] = voronoin ([x, y]);
af = zeros (size(f));
for i = 1 : length (f)
  af(i) = polyarea (c (f {i, :}, 1), c (f {i, :}, 2));
endfor

Facets of the Voronoi diagram with a vertex at infinity have infinity area. A simplified version of polyarea for rectangles is available with rectint

Function File: area = rectint (a, b)

Compute the area of intersection of rectangles in a and rectangles in b. Rectangles are defined as [x y width height] where x and y are the minimum values of the two orthogonal dimensions.

If a or b are matrices, then the output, area, is a matrix where the i-th row corresponds to the i-th row of a and the j-th column corresponds to the j-th row of b.

See also: polyarea.

Function File: [in, on] = inpolygon (x, y, xv, xy)

For a polygon defined by (xv, yv) points, determine if the points (x, y) are inside or outside the polygon. The variables x, y, must have the same dimension. The optional output on gives the points that are on the polygon.

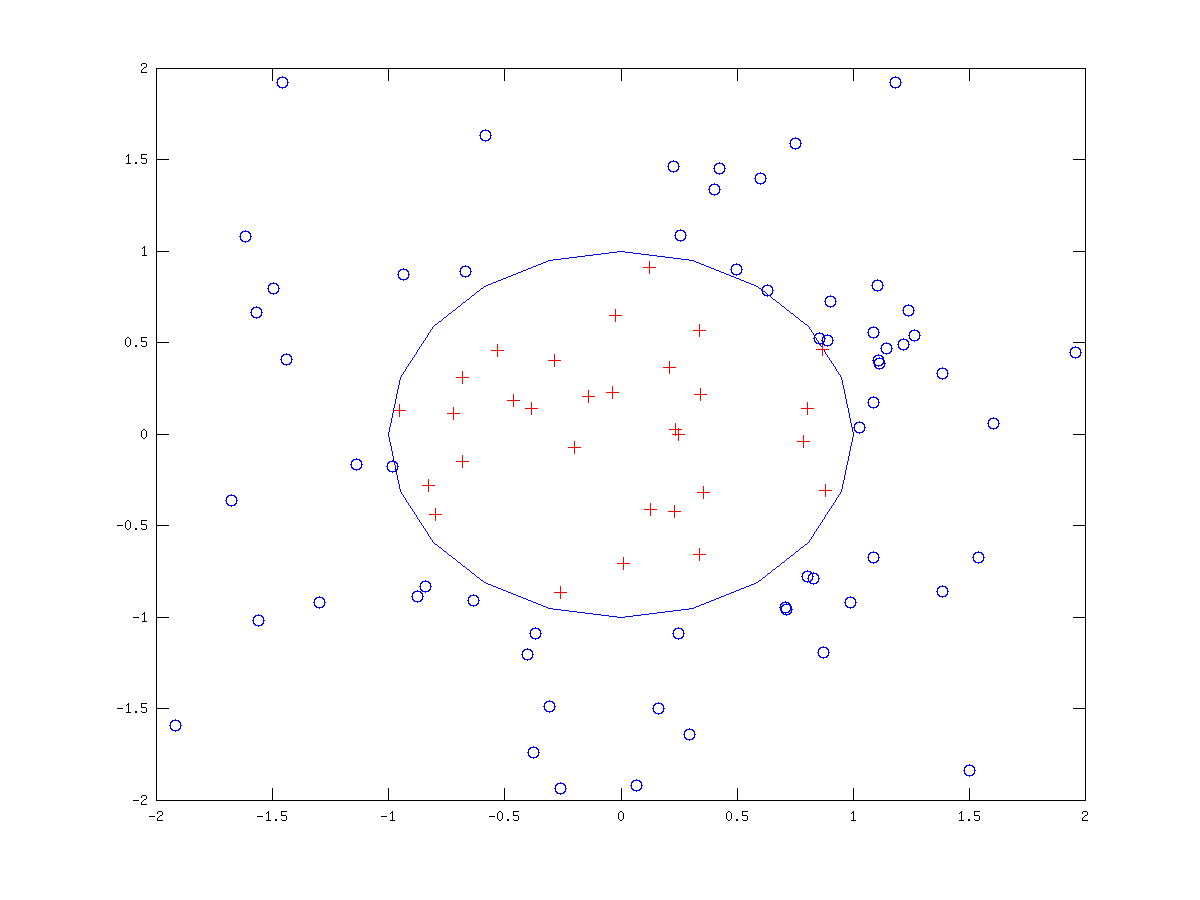
An example of the use of inpolygon might be

randn ("state", 2);
x = randn (100, 1);
y = randn (100, 1);
vx = cos (pi * [-1 : 0.1: 1]);
vy = sin (pi * [-1 : 0.1 : 1]);
in = inpolygon (x, y, vx, vy);
plot(vx, vy, x(in), y(in), "r+", x(!in), y(!in), "bo");
axis ([-2, 2, -2, 2]);

The result of which can be seen in fig:inpolygon.

Figure 29.2: Demonstration of the inpolygon function to determine the points inside a polygon