manpagez: man pages & more
info asymptote
Home | html | info | man
[ << ] [ < ] [ Up ] [ > ] [ >> ]         [Top] [Contents] [Index] [ ? ]

8.27 graph

This package implements two-dimensional linear and logarithmic graphs, including automatic scale and tick selection (with the ability to override manually). A graph is a guide (that can be drawn with the draw command, with an optional legend) constructed with one of the following routines:

An axis can be drawn on a picture with one of the following commands:

Here are some simple examples of two-dimensional graphs:

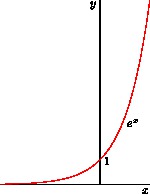
  2. This example draws a textbook-style graph of y= exp(x), with the y axis starting at y=0: 
    import graph;
size(150,0);

real f(real x) {return exp(x);}
pair F(real x) {return (x,f(x));}

xaxis("$x$");
yaxis("$y$",0);

draw(graph(f,-4,2,operator ..),red);

labely(1,E);
label("$e^x$",F(1),SE);

    exp
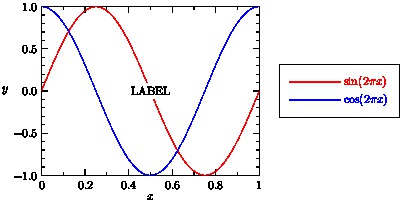
  3. The next example draws a scientific-style graph with a legend. The position of the legend can be adjusted either explicitly or by using the graphical user interface xasy (see section Graphical User Interface). If an UnFill(real xmargin=0, real ymargin=xmargin) or Fill(pen) option is specified to add, the legend will obscure any underlying objects. Here we illustrate how to clip the portion of the picture covered by a label: 
    import graph;

size(400,200,IgnoreAspect);

real Sin(real t) {return sin(2pi*t);}
real Cos(real t) {return cos(2pi*t);}

draw(graph(Sin,0,1),red,"$\sin(2\pi x)$");
draw(graph(Cos,0,1),blue,"$\cos(2\pi x)$");

xaxis("$x$",BottomTop,LeftTicks);
yaxis("$y$",LeftRight,RightTicks(trailingzero));

label("LABEL",point(0),UnFill(1mm));

add(legend(),point(E),20E,UnFill);

    lineargraph0

    To specify a fixed size for the graph proper, use attach: 

    import graph;

size(250,200,IgnoreAspect);

real Sin(real t) {return sin(2pi*t);}
real Cos(real t) {return cos(2pi*t);}

draw(graph(Sin,0,1),red,"$\sin(2\pi x)$");
draw(graph(Cos,0,1),blue,"$\cos(2\pi x)$");

xaxis("$x$",BottomTop,LeftTicks);
yaxis("$y$",LeftRight,RightTicks(trailingzero));

label("LABEL",point(0),UnFill(1mm));

attach(legend(),truepoint(E),20E,UnFill);

    A legend can have multiple entries per line: 

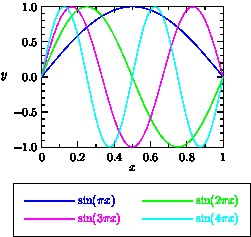
    import graph; 
size(8cm,6cm,IgnoreAspect); 
 
typedef real realfcn(real); 
realfcn F(real p) { 
  return new real(real x) {return sin(p*x);}; 
}; 
 
for(int i=1; i < 5; ++i)
  draw(graph(F(i*pi),0,1),Pen(i),
       "$\sin("+(i == 1 ? "" : (string) i)+"\pi x)$"); 
xaxis("$x$",BottomTop,LeftTicks); 
yaxis("$y$",LeftRight,RightTicks(trailingzero)); 
 
attach(legend(2),(point(S).x,truepoint(S).y),10S,UnFill);

    legend
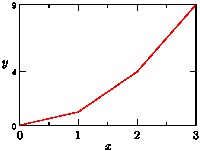
  4. This example draws a graph of one array versus another (both of the same size) using custom tick locations and a smaller font size for the tick labels on the y axis. 
    import graph;

size(200,150,IgnoreAspect);

real[] x={0,1,2,3};
real[] y=x^2;

draw(graph(x,y),red);

xaxis("$x$",BottomTop,LeftTicks);
yaxis("$y$",LeftRight,
      RightTicks(Label(fontsize(8pt)),new real[]{0,4,9}));

    datagraph
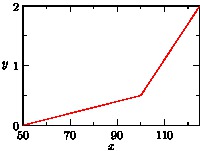
  5. This example shows how to graph columns of data read from a file. 
    import graph;

size(200,150,IgnoreAspect);

file in=input("filegraph.dat").line();
real[][] a=in.dimension(0,0);
a=transpose(a);

real[] x=a[0];
real[] y=a[1];

draw(graph(x,y),red);

xaxis("$x$",BottomTop,LeftTicks);
yaxis("$y$",LeftRight,RightTicks);

    filegraph

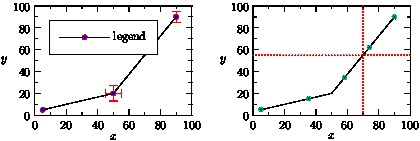
  6. The next example draws two graphs of an array of coordinate pairs, using frame alignment and data markers. In the left-hand graph, the markers, constructed with 
    marker marker(path g, markroutine markroutine=marknodes, 
              pen p=currentpen, filltype filltype=NoFill,
              bool above=true);

    using the path unitcircle (see filltype), are drawn below each node. Any frame can be converted to a marker, using 

    marker marker(frame f, markroutine markroutine=marknodes,
              bool above=true);

    In the right-hand graph, the unit n-sided regular polygon polygon(int n) and the unit n-point cyclic cross cross(int n, bool round=true, real r=0) (where r is an optional “inner” radius) are used to build a custom marker frame. Here markuniform(bool centered=false, int n, bool rotated=false) adds this frame at n uniformly spaced points along the arclength of the path, optionally rotated by the angle of the local tangent to the path (if centered is true, the frames will be centered within n evenly spaced arclength intervals). Alternatively, one can use markroutine marknodes to request that the marks be placed at each Bezier node of the path, or markroutine markuniform(pair z(real t), real a, real b, int n) to place marks at points z(t) for n evenly spaced values of t in [a,b].

    These markers are predefined: 

    marker[] Mark={
  marker(scale(circlescale)*unitcircle),
  marker(polygon(3)),marker(polygon(4)),
  marker(polygon(5)),marker(invert*polygon(3)),
  marker(cross(4)),marker(cross(6))
};

marker[] MarkFill={
  marker(scale(circlescale)*unitcircle,Fill),marker(polygon(3),Fill),
  marker(polygon(4),Fill),marker(polygon(5),Fill),
  marker(invert*polygon(3),Fill)
};

    The example also illustrates the errorbar routines: 

    void errorbars(picture pic=currentpicture, pair[] z, pair[] dp,
               pair[] dm={}, bool[] cond={}, pen p=currentpen,
               real size=0);

void errorbars(picture pic=currentpicture, real[] x, real[] y,
               real[] dpx, real[] dpy, real[] dmx={}, real[] dmy={},
               bool[] cond={}, pen p=currentpen, real size=0);

    Here, the positive and negative extents of the error are given by the absolute values of the elements of the pair array dp and the optional pair array dm. If dm is not specified, the positive and negative extents of the error are assumed to be equal. 

    import graph;

picture pic;
real xsize=200, ysize=140;
size(pic,xsize,ysize,IgnoreAspect);

pair[] f={(5,5),(50,20),(90,90)};
pair[] df={(0,0),(5,7),(0,5)};

errorbars(pic,f,df,red);
draw(pic,graph(pic,f),"legend",
     marker(scale(0.8mm)*unitcircle,red,FillDraw(blue),above=false));

scale(pic,true);

xaxis(pic,"$x$",BottomTop,LeftTicks);
yaxis(pic,"$y$",LeftRight,RightTicks);
add(pic,legend(pic),point(pic,NW),20SE,UnFill);

picture pic2;
size(pic2,xsize,ysize,IgnoreAspect);

frame mark;
filldraw(mark,scale(0.8mm)*polygon(6),green,green);
draw(mark,scale(0.8mm)*cross(6),blue);

draw(pic2,graph(pic2,f),marker(mark,markuniform(5)));

scale(pic2,true);

xaxis(pic2,"$x$",BottomTop,LeftTicks);
yaxis(pic2,"$y$",LeftRight,RightTicks);

yequals(pic2,55.0,red+Dotted);
xequals(pic2,70.0,red+Dotted);

// Fit pic to W of origin:
add(pic.fit(),(0,0),W);

// Fit pic2 to E of (5mm,0):
add(pic2.fit(),(5mm,0),E);

    errorbars
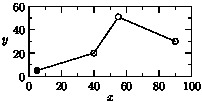
  7. A custom mark routine can be also be specified: 
    import graph;

size(200,100,IgnoreAspect);

markroutine marks() {
  return new void(picture pic=currentpicture, frame f, path g) {
    path p=scale(1mm)*unitcircle;
    for(int i=0; i <= length(g); ++i) {
      pair z=point(g,i);
      frame f;
      if(i % 4 == 0) {
        fill(f,p);
        add(pic,f,z);
      } else {
        if(z.y > 50) {
          pic.add(new void(frame F, transform t) {
              path q=shift(t*z)*p;
              unfill(F,q);
              draw(F,q);
            });
        } else {
          draw(f,p);
          add(pic,f,z);
        }
      }
    }
  };
}

pair[] f={(5,5),(40,20),(55,51),(90,30)};

draw(graph(f),marker(marks()));

scale(true);

xaxis("$x$",BottomTop,LeftTicks);
yaxis("$y$",LeftRight,RightTicks);

    graphmarkers
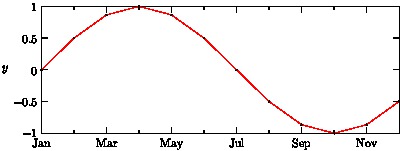
  8. This example shows how to label an axis with arbitrary strings. 
    import graph;

size(400,150,IgnoreAspect);

real[] x=sequence(12);
real[] y=sin(2pi*x/12);

scale(false);

string[] month={"Jan","Feb","Mar","Apr","May","Jun",
                "Jul","Aug","Sep","Oct","Nov","Dec"};

draw(graph(x,y),red,MarkFill[0]);

xaxis(BottomTop,LeftTicks(new string(real x) {
      return month[round(x % 12)];}));
yaxis("$y$",LeftRight,RightTicks(4));

    monthaxis
  9. The next example draws a graph of a parametrized curve. The calls to 
    xlimits(picture pic=currentpicture, real min=-infinity,
        real max=infinity, bool crop=NoCrop);

    and the analogous function ylimits can be uncommented to set the respective axes limits for picture pic to the specified min and max values. Alternatively, the function 

    void limits(picture pic=currentpicture, pair min, pair max, bool crop=NoCrop);

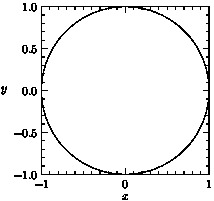
    can be used to limit the axes to the box having opposite vertices at the given pairs). Existing objects in picture pic will be cropped to lie within the given limits if crop=Crop. The function crop(picture pic) can be used to crop a graph to the current graph limits. 

    import graph;

size(0,200);

real x(real t) {return cos(2pi*t);}
real y(real t) {return sin(2pi*t);}

draw(graph(x,y,0,1));

//limits((0,-1),(1,0),Crop);

xaxis("$x$",BottomTop,LeftTicks);
yaxis("$y$",LeftRight,RightTicks(trailingzero));

    parametricgraph

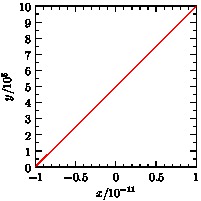
    The next example illustrates how one can extract a common axis scaling factor. 

    import graph;

axiscoverage=0.9;
size(200,IgnoreAspect);

real[] x={-1e-11,1e-11};
real[] y={0,1e6};

real xscale=round(log10(max(x)));
real yscale=round(log10(max(y)))-1;

draw(graph(x*10^(-xscale),y*10^(-yscale)),red);

xaxis("$x/10^{"+(string) xscale+"}$",BottomTop,LeftTicks);
yaxis("$y/10^{"+(string) yscale+"}$",LeftRight,RightTicks(trailingzero));

    scaledgraph

    Axis scaling can be requested and/or automatic selection of the axis limits can be inhibited with one of these scale routines: 

    void scale(picture pic=currentpicture, scaleT x, scaleT y);

void scale(picture pic=currentpicture, bool xautoscale=true,
           bool yautoscale=xautoscale, bool zautoscale=yautoscale);

    This sets the scalings for picture pic. The graph routines accept an optional picture argument for determining the appropriate scalings to use; if none is given, it uses those set for currentpicture.

    Two frequently used scaling routines Linear and Log are predefined in graph.

    All picture coordinates (including those in paths and those given to the label and limits functions) are always treated as linear (post-scaled) coordinates. Use 

    pair Scale(picture pic=currentpicture, pair z);

    to convert a graph coordinate into a scaled picture coordinate.

    The x and y components can be individually scaled using the analogous routines 

    real ScaleX(picture pic=currentpicture, real x);
real ScaleY(picture pic=currentpicture, real y);

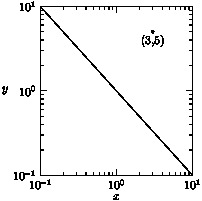
    The predefined scaling routines can be given two optional boolean arguments: automin=false and automax=automin. These default to false but can be respectively set to true to enable automatic selection of "nice" axis minimum and maximum values. The Linear scaling can also take as optional final arguments a multiplicative scaling factor and intercept (e.g. for a depth axis, Linear(-1) requests axis reversal).

    For example, to draw a log/log graph of a function, use scale(Log,Log): 

    import graph;

size(200,200,IgnoreAspect);

real f(real t) {return 1/t;}

scale(Log,Log);

draw(graph(f,0.1,10));

//limits((1,0.1),(10,0.5),Crop);

dot(Label("(3,5)",align=S),Scale((3,5)));

xaxis("$x$",BottomTop,LeftTicks);
yaxis("$y$",LeftRight,RightTicks);

    loggraph

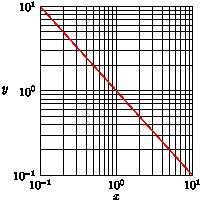
    By extending the ticks, one can easily produce a logarithmic grid: 

    import graph;
size(200,200,IgnoreAspect);

real f(real t) {return 1/t;}

scale(Log,Log);
draw(graph(f,0.1,10),red);
pen thin=linewidth(0.5*linewidth());
xaxis("$x$",BottomTop,LeftTicks(begin=false,end=false,extend=true,
                                ptick=thin));
yaxis("$y$",LeftRight,RightTicks(begin=false,end=false,extend=true,
                                 ptick=thin));

    loggrid

    One can also specify custom tick locations and formats for logarithmic axes: 

    import graph;

size(300,175,IgnoreAspect);
scale(Log,Log);
draw(graph(identity,5,20));
xlimits(5,20);
ylimits(1,100);
xaxis("$M/M_\odot$",BottomTop,LeftTicks(DefaultFormat,
                                        new real[] {6,10,12,14,16,18}));
yaxis("$\nu_{\rm upp}$ [Hz]",LeftRight,RightTicks(DefaultFormat));

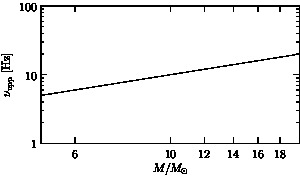
    logticks

    It is easy to draw logarithmic graphs with respect to other bases: 

    import graph;
size(200,IgnoreAspect);

// Base-2 logarithmic scale on y-axis:

real log2(real x) {static real log2=log(2); return log(x)/log2;}
real pow2(real x) {return 2^x;}

scaleT yscale=scaleT(log2,pow2,logarithmic=true);
scale(Linear,yscale);

real f(real x) {return 1+x^2;}

draw(graph(f,-4,4));

yaxis("$y$",ymin=1,ymax=f(5),RightTicks(Label(Fill(white))),EndArrow);
xaxis("$x$",xmin=-5,xmax=5,LeftTicks,EndArrow);

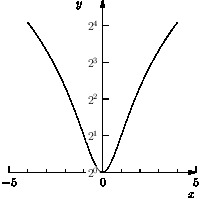
    log2graph

    Here is an example of "broken" linear x and logarithmic y axes that omit the segments [3,8] and [100,1000], respectively. In the case of a logarithmic axis, the break endpoints are automatically rounded to the nearest integral power of the base. 

    import graph;

size(200,150,IgnoreAspect);

// Break the x axis at 3; restart at 8:
real a=3, b=8;

// Break the y axis at 100; restart at 1000:
real c=100, d=1000;

scale(Broken(a,b),BrokenLog(c,d));

real[] x={1,2,4,6,10};
real[] y=x^4;

draw(graph(x,y),red,MarkFill[0]);

xaxis("$x$",BottomTop,LeftTicks(Break(a,b)));
yaxis("$y$",LeftRight,RightTicks(Break(c,d)));

label(rotate(90)*Break,(a,point(S).y));
label(rotate(90)*Break,(a,point(N).y));
label(Break,(point(W).x,ScaleY(c)));
label(Break,(point(E).x,ScaleY(c)));

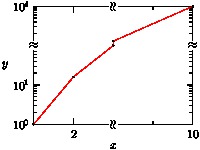
    brokenaxis
  10. Asymptote can draw secondary axes with the routines 
    picture secondaryX(picture primary=currentpicture, void f(picture));
picture secondaryY(picture primary=currentpicture, void f(picture));

    In this example, secondaryY is used to draw a secondary linear y axis against a primary logarithmic y axis: 

    import graph;
texpreamble("\def\Arg{\mathop {\rm Arg}\nolimits}");

size(10cm,5cm,IgnoreAspect);

real ampl(real x) {return 2.5/(1+x^2);}
real phas(real x) {return -atan(x)/pi;}

scale(Log,Log);
draw(graph(ampl,0.01,10));
ylimits(0.001,100);

xaxis("$\omega\tau_0$",BottomTop,LeftTicks);
yaxis("$|G(\omega\tau_0)|$",Left,RightTicks);

picture q=secondaryY(new void(picture pic) {
    scale(pic,Log,Linear);
    draw(pic,graph(pic,phas,0.01,10),red);
    ylimits(pic,-1.0,1.5);
    yaxis(pic,"$\Arg G/\pi$",Right,red,
          LeftTicks("$% #.1f$",
                    begin=false,end=false));
    yequals(pic,1,Dotted);
  });
label(q,"(1,0)",Scale(q,(1,0)),red);
add(q);

    Bode

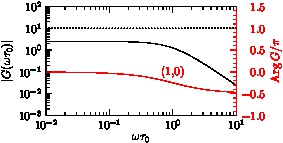
    A secondary logarithmic y axis can be drawn like this: 

    import graph;

size(9cm,6cm,IgnoreAspect);
string data="secondaryaxis.csv";

file in=input(data).line().csv();

string[] titlelabel=in;
string[] columnlabel=in;

real[][] a=in.dimension(0,0);
a=transpose(a);
real[] t=a[0], susceptible=a[1], infectious=a[2], dead=a[3], larvae=a[4];
real[] susceptibleM=a[5], exposed=a[6],infectiousM=a[7];

scale(true);

draw(graph(t,susceptible,t >= 10 & t <= 15));
draw(graph(t,dead,t >= 10 & t <= 15),dashed);

xaxis("Time ($\tau$)",BottomTop,LeftTicks);
yaxis(Left,RightTicks);

picture secondary=secondaryY(new void(picture pic) {
    scale(pic,Linear(true),Log(true));
    draw(pic,graph(pic,t,infectious,t >= 10 & t <= 15),red);
    yaxis(pic,Right,red,LeftTicks(begin=false,end=false));
  });
                             
add(secondary);
label(shift(5mm*N)*"Proportion of crows",point(NW),E);

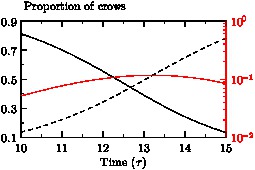
    secondaryaxis
  11. Here is a histogram example, which uses the stats module. 
    import graph;
import stats;

size(400,200,IgnoreAspect);

int n=10000;
real[] a=new real[n];
for(int i=0; i < n; ++i) a[i]=Gaussrand();

draw(graph(Gaussian,min(a),max(a)),blue);

// Optionally calculate "optimal" number of bins a la Shimazaki and Shinomoto.
int N=bins(a);

histogram(a,min(a),max(a),N,normalize=true,low=0,lightred,black,bars=false);

xaxis("$x$",BottomTop,LeftTicks);
yaxis("$dP/dx$",LeftRight,RightTicks(trailingzero));

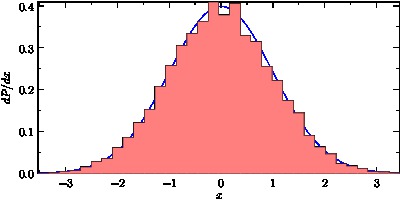
    histogram
  12. Here is an example of reading column data in from a file and a least-squares fit, using the stats module. 
    size(400,200,IgnoreAspect);

import graph;
import stats;

file fin=input("leastsquares.dat").line();

real[][] a=fin.dimension(0,0);
a=transpose(a);

real[] t=a[0], rho=a[1];

// Read in parameters from the keyboard:
//real first=getreal("first");
//real step=getreal("step");
//real last=getreal("last");

real first=100;
real step=50;
real last=700;

// Remove negative or zero values of rho:
t=rho > 0 ? t : null;
rho=rho > 0 ? rho : null;
    
scale(Log(true),Linear(true));

int n=step > 0 ? ceil((last-first)/step) : 0;

real[] T,xi,dxi;

for(int i=0; i <= n; ++i) {
  real first=first+i*step;
  real[] logrho=(t >= first & t <= last) ? log(rho) : null;
  real[] logt=(t >= first & t <= last) ? -log(t) : null;
  
  if(logt.length < 2) break;
  
  // Fit to the line logt=L.m*logrho+L.b:
  linefit L=leastsquares(logt,logrho);
    
  T.push(first);
  xi.push(L.m);
  dxi.push(L.dm);
} 
    
draw(graph(T,xi),blue);
errorbars(T,xi,dxi,red);

crop();

ylimits(0);

xaxis("$T$",BottomTop,LeftTicks);
yaxis("$\xi$",LeftRight,RightTicks);

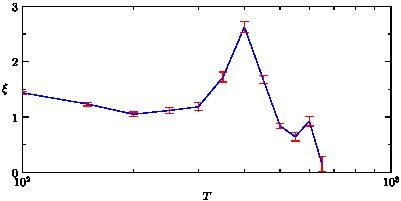
    leastsquares
  13. Here is an example that illustrates the general axis routine. 
    import graph;
size(0,100);

path g=ellipse((0,0),1,2);

scale(true);

axis(Label("C",align=10W),g,LeftTicks(endlabel=false,8,end=false),
     ticklocate(0,360,new real(real v) {
         path h=(0,0)--max(abs(max(g)),abs(min(g)))*dir(v);
         return intersect(g,h)[0];}));

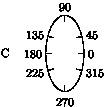
    generalaxis
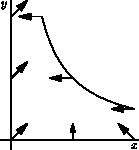
  14. To draw a vector field of n arrows evenly spaced along the arclength of a path, use the routine 
    picture vectorfield(path vector(real), path g, int n, bool truesize=false,
                    pen p=currentpen, arrowbar arrow=Arrow);

    as illustrated in this simple example of a flow field: 

    import graph;
defaultpen(1.0);

size(0,150,IgnoreAspect);

real arrowsize=4mm;
real arrowlength=2arrowsize;

typedef path vector(real);

// Return a vector interpolated linearly between a and b.
vector vector(pair a, pair b) {
  return new path(real x) {
    return (0,0)--arrowlength*interp(a,b,x);
  };
}

real f(real x) {return 1/x;}

real epsilon=0.5;
path g=graph(f,epsilon,1/epsilon);

int n=3;
draw(g);
xaxis("$x$");
yaxis("$y$");

add(vectorfield(vector(W,W),g,n,true));
add(vectorfield(vector(NE,NW),(0,0)--(point(E).x,0),n,true));
add(vectorfield(vector(NE,NE),(0,0)--(0,point(N).y),n,true));

    flow
  15. To draw a vector field of nx\timesny arrows in box(a,b), use the routine 
    picture vectorfield(path vector(pair), pair a, pair b,
                    int nx=nmesh, int ny=nx, bool truesize=false,
                    real maxlength=truesize ? 0 : maxlength(a,b,nx,ny),
                    bool cond(pair z)=null, pen p=currentpen,
                    arrowbar arrow=Arrow, margin margin=PenMargin)

    as illustrated in this example: 

    import graph;
size(100);

pair a=(0,0);
pair b=(2pi,2pi);

path vector(pair z) {return (0,0)--(sin(z.x),cos(z.y));}

add(vectorfield(vector,a,b));

    vectorfield
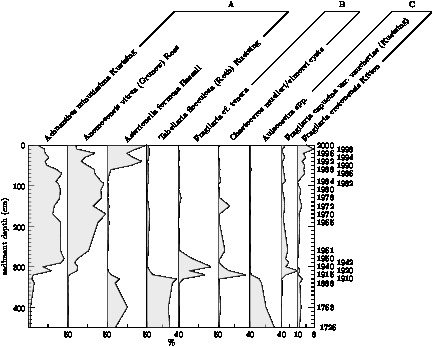
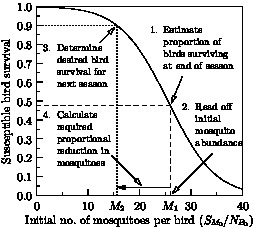
  16. The following scientific graphs, which illustrate many features of Asymptote’s graphics routines, were generated from the examples diatom.asy and westnile.asy, using the comma-separated data in diatom.csv and westnile.csv.
    diatom
    westnile
[ << ] [ < ] [ Up ] [ > ] [ >> ]         [Top] [Contents] [Index] [ ? ]

This document was generated on May 24, 2014 using texi2html 5.0. 

© manpagez.com 2000-2025
Individual documents may contain additional copyright information.